Соедини эти 9 точек четырьмя линиями.
Ну что, у тебя получилось?
Ладно, мы подскажем верное решение. На самом деле их тут аж четыре!
Решение этой головоломки лежит несколько шире нашего стандартного восприятия задачи. Для того, чтобы самостоятельно найти верный подход вспомните, что:
Через любые 2 точки можно провести только одну прямую линию. Прямая линия – это не отрезок и, следовательно, нам не обязательно ограничиваться при рисовании линий нашими девятью синими кружками.
Таким образом, давайте попробуем продолжить линии за пределы, ограничивающего нас до недавнего времени квадрата. Тут видно, что область нашего поиска значительно увеличилась. Потрудившись немного можно прийти к одному из правильных решений.
Последовательность соединений девяти точек четырьмя линиями:
Для начала проведите линию, соединяющую точку №1 и точку №7, через точку №4. Не останавливайте движение и рисуйте дальше примерно столько, сколько от точки №4 до точки №7.
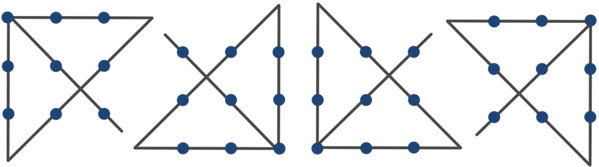
Далее двигайтесь по диагонали направо-вверх, соединяя точки №8 и №6. Не останавливайтесь на точке №6 и продолжайте линию до мысленной прямой, проходящей через верхнюю сторону нашего квадрата.
Нарисуйте линию справа налево последовательно через точки №3, №2 и №1. Остановитесь на точке №1.
Теперь проведите финальный отрезок через точки №1, №5 и №9. Все 9 точек, и правда, соединены четырьмя линиями, как и требовалось в условии задачи.
Другие варианты. Этот способ не единственный, начинать можно от любого угла и двигаться одном из двух направлений.
